高阶，方程组等进阶内容

虽然是高阶，但是可以直接积分，多积分几次就可以了

只有n阶和n-1阶（y没有出现），替换变量，化成可以分离变量的形式

x没有出现，利用链式法则处理，思路还是消除变量，达到可以分离变量的程度

1. 线性：y的各阶导数之间是相加的关系（没有相乘等运算）/对于y及其各阶导数是线性的（没有y及其各阶导数之间的相互乘积）
2. 常系数：y的导数的各项的系数是常数（和x无关）/y及其各阶导数前面的系数是否为常数（还是一个式子）
3. 齐次：是不是0/除y及其各阶导数以外的部分，是0（非齐次就是不是0）

有定理12

定理1:

证明定理1：代入即可。但是$c_1y_1+c_2y_2$不一定是方程的通解。

定理2:当$y_1$和$y_2$线性无关时，$c_1y_1+c_2y_2$是方程的通解。（如果线性相关，常数就可以合并了，不符合通解的定义）
线性无关：二者做比，比值包含x，比如$x^2$和$x$（线性无关）；比较不包含x，是个常数，比如$x^2$和$2x^2$（线性相关）。
定理2可以推广至n阶线性微分方程，比如3阶线性微分方程对应$c_1y_1+c_2y_2+c_3y_3$

Q：通解（一般解）的定义是？包含N个不能合并的任意常数的解
特解：满足方程但是不包含任意常数。

定理3：式子中（1）表示的是对应的齐次方程

代入：式子成立，可证明$Y+y^{*}$是方程组的解。然后，$Y$中有两个不可合并的任意常数，$y^{*}$中没有，所以一共包含两个不可合并的任意常数，所以是通解。

根据定理3，我们可以得到，求解高阶线性非齐次微分方程的一个思路：

用处：找非齐次线性微分方程的解（这里求出来的是通解吗？）（以上用定理3的思路求解非齐次线性微分方程的步骤2）

大概流程：

假设对应的齐次方程的通解是：$c_1y_1+c_2y_2$
设：$u_1y_1+u_2y_2$为非齐次的一个解

将$y=u_1y_1+u_2y_2$代入非齐次方程
代入之前加一个约束条件
得到$y^{\prime}$和$y^{\prime\prime}$

代入方程后，消除一部分
消除的根据是：$y_1$和$y_2$都是齐次方程的解
即可得到一个方程

上面添加过一个约束条件，和刚才得到的方程一起组成一个方程组
最终得到一个方程组，即可解得$u_1^{\prime}$和$u_2^{\prime}$，再积分即可

特征根
基本思路：设方程的解为$e^{{\lambda}x}$，代入即可，即可得到关于$\lambda$的方程（一元二次方程，特征方程）

对于以上结果

1. 两个不同的实数根的情况很好理解
2. 对于重根的情况，可以使用常数变易法找到另一个解（课件中有详细的推导）
3. 对于没有实数根的情况，其实和第一种情况类似，只是化简了一下，变成了三角函数的形式（欧拉函数）

以上内容都可推导至n阶，解的情况如下（最后各个根对应的解都加起来就行了，课件中有一道例题）：

可以类比非常系数非齐次情况的定理3（参照上文）
先找齐次的通解，再找到非齐次的一个特解

那么如何找非齐次的特解呢？

首先，可以根据右边的$f(x)$的形式“猜一下”：

情况1：

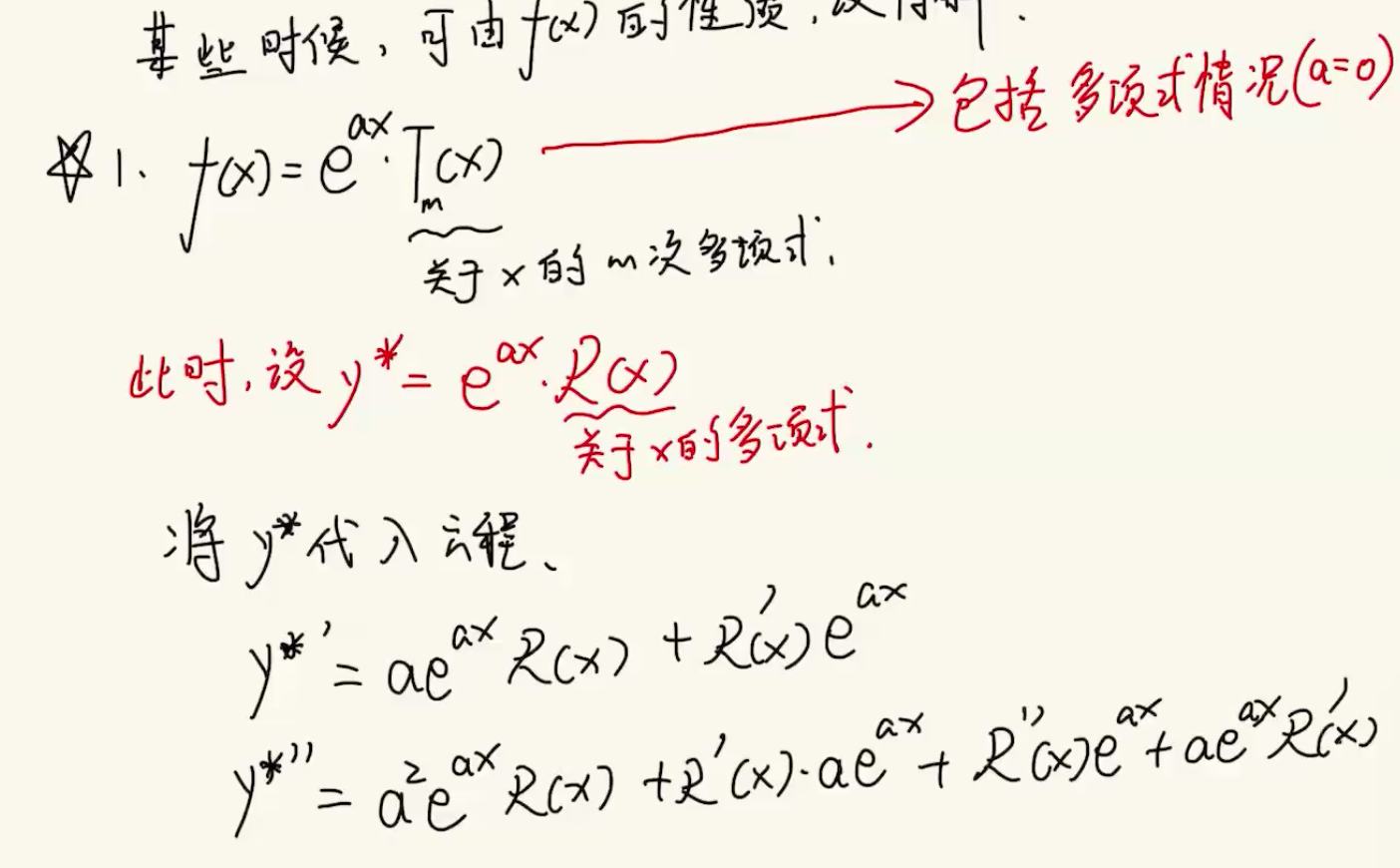
找到$R(x)$应该是几次多项式，然后设其系数，再代回（原微分方程）求解（有一定的计算量）（还是要看一下例题）

不是常系数；有方法处理，一般形式如下：

代入后即可解得$\lambda$的值，然后得到微分方程的解（分以下情况讨论）

和偏微分方程不是同一个东西

要理解微分算子，以下只是举个例子（这道题好像用微分算子不好做）